引言

  • 使用上下文无关文法引导语言的翻译
    • CFG的非终结符号代表了语言的某个构造
    • 程序设计语言的构造由更小的构造组合而成
    • 一个构造的语义可以由小构造的含义综合而来
      • 比如：表达式x+y的类型由x、y的类型和运算符+决定
    • 也可以从附近的构造继承而来
      • 比如：声明int x;中x的类型由它左边的类型表达式决定

语法制导定义和语法制导翻译

语法制导定义

  • 逆波兰表达式，英文为 Reverse Polish notation，跟波兰表达式（Polish notation） 相对应
  • 波兰的数理科学家 Jan Łukasiewicz 发明
    • 中缀表达式: (1 + 2) * (3 + 4)加减乘除等运算符写在中间
    • 波兰表达式: (* (+ 1 2) (+ 3 4))，将运算符写在前面，因而也称为前缀表达式
    • 逆波兰表达式: ((1 2 +) (3 4 +) *)，将运算符写在后面， 因而也称为后缀表达式

语法制导翻译

  • 在产生式体中加入语义动作，并在适当的时候执行这些语义动作

语法制导的定义（SDD）

  • SDD是对上下文无关文法的推广
    • 将每个文法符号和一个语义属性集合相关联
    • 将每个产生式和一组语义规则相关联，这些规则用于计算该产 生式中各文法符号的属性值
  • SDD是上下文无关文法和属性/规则的结合
    • 属性和文法符号相关联，按照需要来确定各个文法符号需要哪些属性
    • 规则和产生式相关联
    • 主要就是为CFG中的文法符号设置语义属性，具体来说，主要就是将一些语义属性附加到代表语言构造的文法符号上，从而把信息和语言构造联系起来
  • 对于文法符号X和属性a，用X.a表示分析树中的某个标号为X的结点的值
  • 一个分析树结点和它的分支对应于一个产生式规则，而对应的语义规则确定了这些结点上的属性的取值

分析树和属性值

  • 假设我们需要知道一个表达式的类型，以及对应代码将它的值存放在何处，我们就需要两个属性：type，place
  • 产生式规则
  • 语义规则（假设只有int/float类型）
  • 产生式规则：F→id
  • 例

继承属性和综合属性

综合属性(synthesized attribute)

  • 在分析树结点N上的非终结符号A的属性值由N对应的产生式所关联的语义规则来定义
    • 通过N的子结点或N本身的属性值来定义

继承属性(inherited attribute)

  • 结点N的属性值由N 的父结点所关联的语义规则来定义
    • 依赖于N的父结点、N本身和N的兄弟结点上的属性值

S属性的SDD和L属性的SDD

S属性的SDD

  • 只包含综合属性的SDD称为S属性的SDD
    • 每个语义规则都根据产生式体中的属性值来计算头部非终结符号的属性值
  • S属性的SDD可以和LR语法分析器一起实现
    • 栈中的状态可以附加相应的属性值
    • 在进行归约时，按照语义规则计算归约得到的符号的属性值
  • 语义规则不应该有复杂的副作用
    • 要求副作用不影响其它属性的求值
    • 没有副作用的SDD称为属性文法

L属性的SDD

语法分析树上的SDD求值

  • 实践中很少先构造语法分析树再进行SDD求值
  • 但在分析树上求值有助于翻译方案的可视化，便于理解
  • 注释语法分析树
    • 包含了各个结点的各属性值的语法分析树
  • 步骤：
    • 对于任意的输入串，首先构造出相应的分析树。
    • 给各个结点（根据其文法符号）加上相应的属性值
    • 按照语义规则计算这些属性值即可
  • 按照分析树中的分支对应的文法产生式，应用相应的语义规则计算属性值
  • 如果我们可以给各个属性值排出计算顺序，那么这个注释分析树就可以计算得到
    • S属性的SDD一定可以按照自底向上的方式求值
  • 下面的SDD不能计算

适用于自顶向下分析的SDD

  • 左递归文法无法直接用自顶向下方法处理

SDD的求值顺序

  • 使用依赖图来表示计算顺序
  • 显然，这些值的计算顺序应该形成一个偏序关系。如果依赖图中出现了环，表示属性值无法计算

依赖图

例子

属性值的计算顺序

  • 各个属性的值需要按照依赖图的拓扑顺序计算
    • 如果依赖图中存在环，则属性计算无法进行
  • 给定一个SDD，很难判定是否存在一棵分析树，其对应的依赖图包含环
  • 怎样的SDD可以和以前所介绍的语法分析结合在一起？
  • 特定类型的SDD一定不包含环，且有固定排序模式
    • S属性的SDD
    • L属性的SDD
  • 对于这些类型的SDD，我们可以确定属性的计算顺序，且可以把不需要的属性（及分析树结点）抛弃以提高效率
  • 这两类SDD可以很好地和我们已经研究过的语法分析相结合

S属性的SDD

  • 每个属性都是综合属性
  • 都是根据子构造的属性计算出父构造的属性
  • 在依赖图中，总是通过子结点的属性值来计算父结点的属性值。可以和自顶向下、自底向上的语法分析过程一起计算
    • 自底向上
      • 在构造分析树的结点的同时计算相关的属性（此时其子结点 的属性必然已经计算完毕）
    • 自顶向下
      • 递归下降分析中，可以在过程A()的最后计算A的属性（此时 A调用的其他过程（对应于子结构）已经调用完毕）

在分析树上计算SDD

  • 按照后序遍历的顺序计算属性值即可
  • 在LR分析过程中，我们实际上不需要构造分析树的结点

L属性的SDD

  • 每个属性
  • 特点
    • 依赖图的边
      • 继承属性从左到右，从上到下
      • 综合属性从下到上
    • 在扫描过程中，计算一个属性值时，和它相关的依赖属性都已经计算完毕

具有受控副作用的语义规则

  • 属性文法没有副作用，但增加了描述的复杂度
    • 比如语法分析时如果没有副作用，标识符表就必须作为属性传递
    • 可以把标识符表作为全局变量，然后通过副作用函数来添加新标识符
  • 受控的副作用
    • 不会对属性求值产生约束，即可以按照任何拓扑顺序求值，不会影响最终结果
    • 或者对求值过程添加简单的约束

受控副作用的例子

语法制导翻译的应用例子

构造抽象语法树的SDD

  • 抽象语法树
    • 每个结点代表一个语法结构；对应于一个运算符
    • 结点的每个子结点代表其子结构；对应于运算分量
    • 表示这些子结构按照特定方式组成了较大的结构
    • 可以忽略掉一些标点符号等非本质的东西
  • 语法树的表示方法
    • 每个结点用一个对象表示
    • 对象有多个域
      • 叶子结点中只存放词法值
      • 内部结点中存放了op值和参数（通常指向其它结点）

构造简单表达式的语法树的SDD

表达式语法树的构造过程

自顶向下方式处理的L属性定义

  • 对于这个SDD，各属性值的计算过程实际上和原来S属性定义中的计算过程一致
  • 继承属性可以把值从一个结构传递到另一个并列的结构；也可把值从父结构传递到子结构
  • 抽象语法树和分析树不一致时，继承属性很有用

基本类型和数组类型的L属性定义

类型结构

类型的含义

类型表达式的生成过程

语法制导的翻译方案

  • 语法制导的翻译方案（SDT）是在产生式体中嵌入程序片断（语义动作）的上下文无关文法
  • SDT的基本实现方法
    • 建立语法分析树
    • 将语义动作看作是虚拟的结点
    • 从左到右、深度优先地遍历分析树，在访问虚拟结点时执行相应动作

在语法树上实现SDT

可在语法分析过程中实现的SDT

  • 实现SDT时，实际上并不会真的构造语法分析树，而是在分析过程中执行语义动作
  • SDT可以看做是SDD的具体实施方案
  • 即使基础文法可以应用某种分析技术，仍可能因为动作的缘故（例如属性计算过程中的循环依赖）导致此技术不可应用
  • 用SDT实现两类重要的SDD
    • 基本文法可以使用LR分析技术，且SDD是S属性的
    • 基本文法可以使用LL分析技术，且SDD是L属性的
  • 判断是否可在分析过程中实现
    • 将每个语义动作替换为一个独有的标记非终结符号；每个标记非终结符号M的产生式为M → ε
    • 如果新的文法可以由某种方法进行分析，那么这个SDT就可以在这个分析过程中实现
    • 注意：这个方法没有考虑变量值的传递等要求

将S属性的SDD转换为SDT

  • 非常简单，由于S属性的SDD中，所有的属性均为综合属性，因此，只有当所有子属性计算完毕之后，才能计算父节点
  • 因此，我们只需要把所有的语义规则放到对应产生式的右部即可

将L属性的SDD转换为SDT

  • 将计算某个非终结符号A的继承属性的动作插入到产生式右部中紧靠在A的本次出现之前的位置上；
  • 将计算一个产生式左部符号的综合属性的动作放置在这个产生式右部的最右端
  • 如果一个L属性的SDD的基本文法可以使用LL分析技术，那么它的SDT可以在LL或者LR语法分析过程中实现

判断SDT可否用特定分析技术实现例子

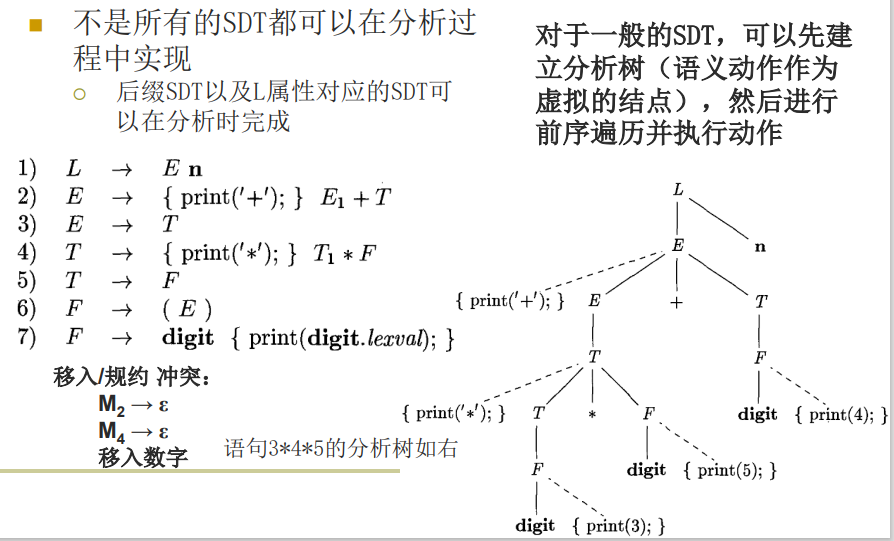
后缀翻译方案

  • 后缀SDT：所有动作都在产生式最右端的 SDT
  • 文法可以自底向上分析且SDD是S属性的，必然可以构造出后缀SDT
  • 构造方法
    • 将每个语义规则看作是一个赋值语义动作
    • 将所有的语义动作放在规则的最右端

后缀翻译方案的例子

后缀SDT的语法分析栈实现

  • 可以在LR语法分析的过程中实现
    • 归约时执行相应的语义动作
    • 定义用于记录各文法符号的属性的union结构
    • 栈中的每个文法符号（或者说状态）都附带一个这样的union类型的值
    • 在按照产生式A → XYZ归约时，Z的属性可以在栈顶找到，Y的属性可以在下一个位置找到，X的属性可以在再下一个位置找到

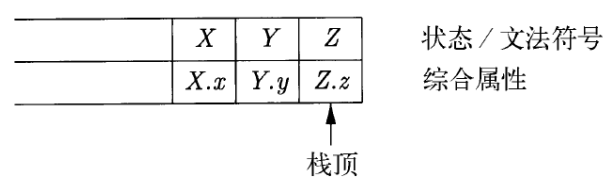
分析栈实现的例子

  • 假设语法分析栈存放在一个被称为stack的记录数组中，下标top指向栈顶
    • stack[top]是这个栈的栈顶
    • stack[top-1]指向栈顶下一个位置
    • 如果不同的文法符号有不同的属性集合，我们可以使用union来保存这些属性值
      • 归约时能够知道栈顶向下的各个符号分别是什么, 因此我们也能够确定各个union中究竟存放了什么样的值

后缀SDT的栈实现

产生式内部带有语义动作的SDT

  • 动作左边的所有符号（以及动作）处理完成后，就立刻执行这个动作
    • B → X{a}Y
    • 自底向上分析时，在X出现在栈顶时执行动作a
    • 自顶向下分析时，在试图展开Y或者在输入中检测到Y的时刻执行a

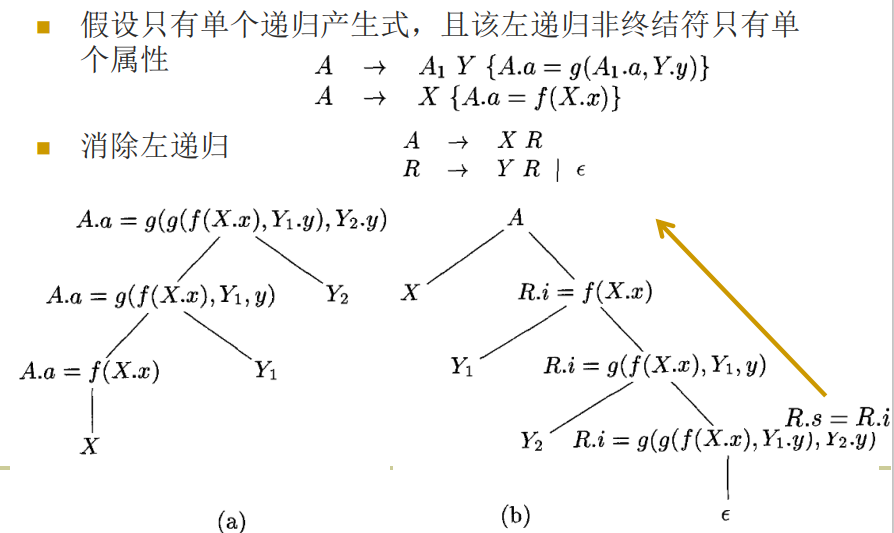
从SDT中消除左递归

消除左递归时SDT的转换

  • 如果动作不涉及属性值，可以把动作当作 终结符号进行处理，然后消左递归
  • 原始的产生式
  • 转换后得到

消除左递归时SDT的一般转换形式

L属性定义的SDT

  • 将L属性的SDD转换为SDT
    • 将每个语义规则看作是一个赋值语义动作
    • 将赋值语义动作放到相应产生式的适当位置
      • 计算A的继承属性的动作插入到产生式体中对应的A的左边
        • 如果A的继承属性之间具有依赖关系，则需要对计算动作进行排序
      • 计算产生式头的综合属性的动作在产生式的最右边

实例

  • SDD
  • 继承属性：
    • next：语句结束后应该跳转到的标号
    • true、false：C为真/假时应该跳转到的标号
  • 综合属性code表示代码

将SDD转换为SDT

  • 语义动作
    • (a) L1=new( )；L2=new( )：计算临时值
    • (b) C.false = S.next; C.true = L2：计算C的继承属性
    • (c) S1.next = L1：计算S1的继承属性
    • (d) S.code= …：计算S的综合属型
  • 根据放置语义动作的规则得到如下SDT
    • (b)在C之前；(c)在S1之前；(d)在最右端
    • (a)可以放在最前面

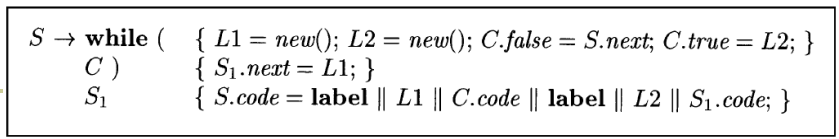
L属性的SDD的实现

  • 使用递归下降的语法分析器
    • 每个非终结符号对应一个函数
    • 函数的参数接受继承属性
    • 返回值包含了综合属性
  • 在函数体中
    • 首先选择适当的产生式
    • 使用局部变量来保存属性
    • 对于产生式体中的终结符号，读入符号并获取其（经词法分析得到的）综合属性
    • 对于非终结符号，使用适当的方式调用相应函数，并记录返回值

递归下降法实现L属性SDD的例子

边扫描边生成属性

  • 当属性值的体积很大时，对属性值进行运算的效率很低
    • 比如code（代码）可能是一个上百K的串，对其进行并置等运算会比较低效
  • 可以逐步生成属性的各个部分，并增量式添加到最终的属性值中
  • 条件：
    • 存在一个主属性，且主属性是综合属性
    • 在各产生式中，主属性是通过产生式体中各个非终结符号的主属性连接（并置）得到的，同时还会连接一些其它的元素
    • 各非终结符号的主属性的连接顺序和它在产生式体中的顺序相同
  • 基本思想
    • 只需要在适当的时候“发出”非主属性的元素，即把这些元素拼接到适当的地方
  • 举例说明
    • 假设我们在扫描一个非终结符号对应的语法结构时，调用相应的函数，并生成主属性
    • S → while (C) S1
      • S.code = Label || L1 ||C.code ||Label || L2 || S1.code
    • 处理S时，先调用C，再调用S（对应于S1）
    • 如果各个函数把主属性打印出来，我们处理while语句时，只需要先打印Label L1，再调用C（打印了C的代码），再打印Label L2，再调用S（打印S1的代码）
    • 对于这个规则而言，只需要打印Label L1和Label L2，当然，我们要求C和S的语句在相应情况下跳转到L1和L2

边扫描边生成属性的例子