图的遍历

BFS

需要借助一个队列来非递归实现

DFS

递归实现

最小生成树（MST）-贪心思想

Prim算法

从某一个顶点开始构建生成树；每次将代价最小的新顶点纳入生成树，直到所有顶点都纳入为止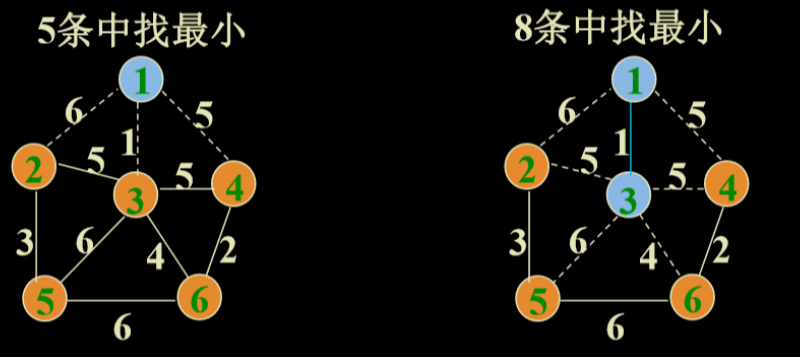


  • 时间复杂度 $O(\vert V^2 \vert )$
  • 适合用于边稠密图

Kruskal算法

每次选择一条权值最小的边，将这条边的两头连通（原本已经连通的就不选），直到所有结点都连通

  • 时间复杂度 $O(\vert E \vert \log_2 \vert E \vert )$
  • 适合用于边稀疏图

最短路径问题

  • 单源最短路径问题
  • 每对顶点间的最短路径

    BFS算法求单源最短路径

    Dijkstra算法求带非负权值图单源最短路径

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    /**
    	path数组记录从源节点这一节点到目标结点路径上的倒数第二个节点，以此类推
    	dist数组记录到该点的当前已知最短路径长度
    	s记录该点是否已经加入已选点集中
    	图用邻接矩阵表示
    **/
    public int[] shortestpath(int v){
    	//v为源点数值
        int n = this.numOfVertex;
        // 初始化
        for( int i=0; i<n; i++){
            dist[i]=Edge[v][i]; //dist初始化 
            s[i]=0; //s为check数组，记录每个顶点是否被访问过
            if( i!=v && dist[i]< MAXNUM ) path[i]=v;
            else path[i]=-1;
        }
        s[v]=1; //源点已访问
        dist[v]=0; //源点到自身距离为0
        for( i=0; i<n-1; i++){
            float min=MAXNUM; 
            int u = v;
            // 找出最近的点集
            for( int j=0; j<n; j++)
                if( !s[j] && dist[j]<min ) { //找未被访问过且最小的顶点
                    u=j; 
                    min=dist[j];
                }
                s[u]=1; //把这个最近的点纳入已知点集中
            // 更新距离
            for ( int w=0; w<n; w++)
                if( !s[w] && Edge[u][w] < MAXNUM && dist[u] + Edge[u][w] < dist[w]){ //未被访问过 && u和w间有边 && 从u到w比之前到w的路要短
                    // 只需要考虑未被加入点集中的点
                    dist[w]=dist[u]+Edge[u][w]; 
                    path[w]=u;
                }
        }
        return path;
    }

    Bellman-Ford算法

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    public int[] BellmanFord(int v){ //v是源点
        int n = this.numOfVertex;
        for(int i=0;i<n;i++){ 
            dist[i]=Edge[v][i]; //初始化dist
            if(i!=v&&dist[i]<MAXNUM)
                path[i]=v;
            else path[i]=-1;
        }
        for (int k=2;k<n;k++) // 事实上可以不做满这么多次，当你发现距离数组已经不变化的时候就可以不做了
            for(int u=0;u<n;u++)
                if(u!=v) //若u不是源点
                    for(i=0;i<n;i++) 
                        if (Edge[i][u] >0 && Edge[i][u]<MAXNUM && dist[u]>dist[i]+Edge[i][u]){
    	                    //若边不为负权 && i与u之间有边 && 走i-u到u的距离比u原先的dist短
                            dist[u]=dist[i]+Edge[i][u];
                            path[u]=i;
                        }
        return path;
    }

Floyed算法-动态规划思想

不能解决带有“负权回路”的图
三层暴力for循环遍历